7. Testing Goodness-of-fit and Independence
1 Univariate Distributions
We will discuss a method to test the null-hypothesis that the population distribution is some pre-specified member of the family of Multinomial distributions. For instance: somebody claims to know that 50%50% of the people go to work by car, 10%10% go to work by car-pooling, 20%20% go to work by train and 20%20% go to work by bus. This null-hypothesis can be formulated as follows:
- Let XX be a random variable whose distribution is a member of the family of multinomial distributions with four groups (k=4k=4).
- The null-hypothesis is: H0:p1=0.5,p2=0.1,p3=0.2H0:p1=0.5,p2=0.1,p3=0.2, p4=0.2p4=0.2.
- The alternative hypothesis is: H1:otherwiseH1:otherwise.
The dataset Mode (from the Ecdat package) has n=453n=453 observations. Each person answered some questions concerning commuting to work. The variable choice is the variable we are interested in here. We show the first 10 observations of the dataset:
library(Ecdat)
data(Mode)
attach(Mode) #attach the dataset. choice is the variable we want.
library(DT)
library(widgetframe)
dt <- datatable(Mode, caption = "The Raw Data")
frameWidget(dt, height = 550) #only necessary in Hugo Academic webpagesWe do not need all the 453453 observations on the variable choice: all we need to know is the number of people that are observed in each of the 4 groups. These numbers are called frequencies or counts.
Obs_counts <- table(choice)
Obs_counts## choice
## car carpool bus rail
## 218 32 81 122Based on these 4 numbers, should we reject the null-hypothesis?
- Our data is O1=218O1=218, O2=32O2=32, O3=81O3=81 and O4=122O4=122.
- How many people do we expect to observe in group 1 if H0H0 is true? E1=n×p1=453×0.5=226.5E1=n×p1=453×0.5=226.5.
- How many people do we expect to observe in group 2 if H0H0 is true? E2=n×p2=453×0.1=45.3E2=n×p2=453×0.1=45.3.
- How many people do we expect to observe in group 3 if H0H0 is true? E3=n×p3=453×0.2=90.6E3=n×p3=453×0.2=90.6.
- How many people do we expect to observe in group 4 if H0H0 is true? E4=n×p4=453×0.2=90.6E4=n×p4=453×0.2=90.6.
We can test the null-hypothesis using the Q-statistic:
Q=k∑i=1(Oi−Ei)2Eiapprox∼H0χ2k−1.Q=k∑i=1(Oi−Ei)2Eiapprox∼H0χ2k−1.
We reject the null-hypothesis when QQ is too large: in that case, the OiOi’s are very different from the EiEi’s, so that the numerator becomes a large positive number (we only divide by EiEi so that finding RSD(Q) is easier).
When is QQ large enough to reject the null-hypothesis? It can be shown that, under H0H0, the repeated sampling distribution of QQ is the so-called chi-squared distribution with k−1k−1 degrees of freedom. The decision-rule is therefore:
Reject the null-hypothesis when QobsQobs is larger than qχ2k−10.95qχ2k−10.95.
We often make assumptions like the following: the population distribution is a member of the family of Poisson distributions with (unknown) parameter λλ. We can use the Q-statistic (or: the chi-squared test) to test this hypothesis as well:
- We first estimate the unknown parameters (by Maximum Likelihood). Here we have one unknown parameter (λλ) so that e=1e=1.
- Suppose that ˆλ=2^λ=2. We can now test the null-hypothesis that XX has a Poisson distribution with λ=2λ=2 using the Q-statistic.
- As λλ was estimated (instead of it being known), we have more uncertainty than before. The approximate repeated sampling distribution of the QQ statistic if the null hypothesis is true is now the χ2k−1−eχ2k−1−e distribution: we use degrees of freedom equal to k−2k−2 instead of k−1k−1 in this example.
We can also use the chi-squared test to test null-hypotheses with continuous distributions: all we have to do is discretise the continuous distribution to obtain a multinomial distribution. We can then apply the test using the multinomial null-hypothesis. Again, if the distribution has unknown parameters, we estimate them before discretising.
Chi-squared Test: The Method (Univariate)
- step 1: specify H0H0, possibly after first estimating ee parameters (and discretising if XX is continuous): a Multinomial distribution with kk groups.
- step 2: Calculate Ei=npiEi=npi, the expected frequencies if H0H0 is true, for i=1,…,ki=1,…,k. For each ii, we need Ei≥5Ei≥5.
- step 3: Calculate Qobs=∑ki=1(Oi−Ei)2EiQobs=∑ki=1(Oi−Ei)2Ei and reject H0H0 if Qobs>qχ2k−1−e0.95Qobs>qχ2k−1−e0.95.
The method is best explained by applying it to some examples. There are several types of situations to consider:
- Is the distribution under the null-hypothesis (a) discrete or (b) continuous?
- Is the distribution under the null-hypothesis (1) completely known or (2) does it contain unknown parameters?
This leads to four possible cases, 1a, 1b, 2a and 2b. We will discuss an example for each of those.
1.1 Case 1a: Known Discrete Distribution
- apply the Chi-squared test directly with e=0e=0
- Make sure that that Ei≥5Ei≥5 for i=1,2,…,ki=1,2,…,k.
Suppose that the null-hypothesis is H0:X∼Poisson(λ=2)H0:X∼Poisson(λ=2). It is up to the researcher (you) how many groups to use. In this example, we could define the 9 groups as “group i consists of the people with X=i−1X=i−1 for i=1,2,…,9i=1,2,…,9”. This occurs because P(X=x)P(X=x) is only positive for x=0,1,…8x=0,1,…8:
round(dpois(0:10, 2), 3)## [1] 0.135 0.271 0.271 0.180 0.090 0.036 0.012 0.003 0.001 0.000 0.000To be precise, we actually take group 9 to contain the people with X≥8X≥8. This grouping is problematic for the following reason: the EiEi’s must always be larger or equal to 5. If some EiEi’s are smaller than 5, the RSD of Q is not well-approximated by the chi-squared distribution, it turns out (this is not obvious).
As an example, we draw a random sample of size n=50n=50 from the Poisson(λ=3λ=3) distribution (so the null-hypothesis is false), and calculate the frequencies:
set.seed(1234)
data <- rpois(50, lambda=3)
O <- table(data)
O## data
## 0 1 2 3 4 5 6 8
## 3 4 16 14 7 4 1 1These are the 0i0i’s. If the null-hypothesis is true, our expectations about the frequencies are described by the EiEi’s. For n=50n=50, we obtain:
E <- 50*dpois(0:10, lambda=2)
round(E, 3)## [1] 6.767 13.534 13.534 9.022 4.511 1.804 0.601 0.172 0.043 0.010
## [11] 0.002As E5=4.511≤5E5=4.511≤5, we need to reduce the number of groups to k=5k=5. A person will be part of group 5 if X≥4X≥4 (instead of X=4X=4). The corresponding probability is P(X≥4)=1−P(X≤3)=0.1428P(X≥4)=1−P(X≤3)=0.1428. The new E5E5 is therefore equal to 50×0.1428=7.14≥550×0.1428=7.14≥5.
Using the new grouping, the observed Q-statistic is equal to:
O_new <- c(O[1:4], sum(O[5:8]))
O_new## 0 1 2 3
## 3 4 16 14 13E_new <- c( E[1:4], sum(E[5:11]) )
E_new## [1] 6.766764 13.533528 13.533528 9.022352 7.143412Q_obs <- sum( (O_new - E_new)^2/E_new )
Q_obs## [1] 16.80984qchisq(0.95, df=4)## [1] 9.487729As Qobs=16.81>9.48Qobs=16.81>9.48, we (correctly) reject the null-hypothesis that λ=2λ=2.
We could also have let R calculate everything for us, using the command chisq.test:
#poisson(2) null-hypothesis probabilities:
p=dpois(0:3, lambda=2)
p## [1] 0.1353353 0.2706706 0.2706706 0.1804470sum(p)## [1] 0.8571235#Chi-squared-test:
chisq.test(x=c(3, 4, 16, 14, 13),
p=c(p, 1-sum(p)) )##
## Chi-squared test for given probabilities
##
## data: c(3, 4, 16, 14, 13)
## X-squared = 16.809, df = 4, p-value = 0.0021051.2 Case 1b: Known Continuous Distribution
- discretise to k categories
- apply Chi-squared test with e=0e=0
Suppose that we want to test the null-hypothesis that X∼Exp(λ=0.2)X∼Exp(λ=0.2). The mean of this distribution is equal to 55 and the variance is equal to 2525. We make a quick plot:
x <- 0:20
prob <- dexp(x, rate=0.2)
plot(x=x, y=prob, type ="l", col="red", xlab="x",
ylab="Expl(0.2)", ylim=c(0,0.3))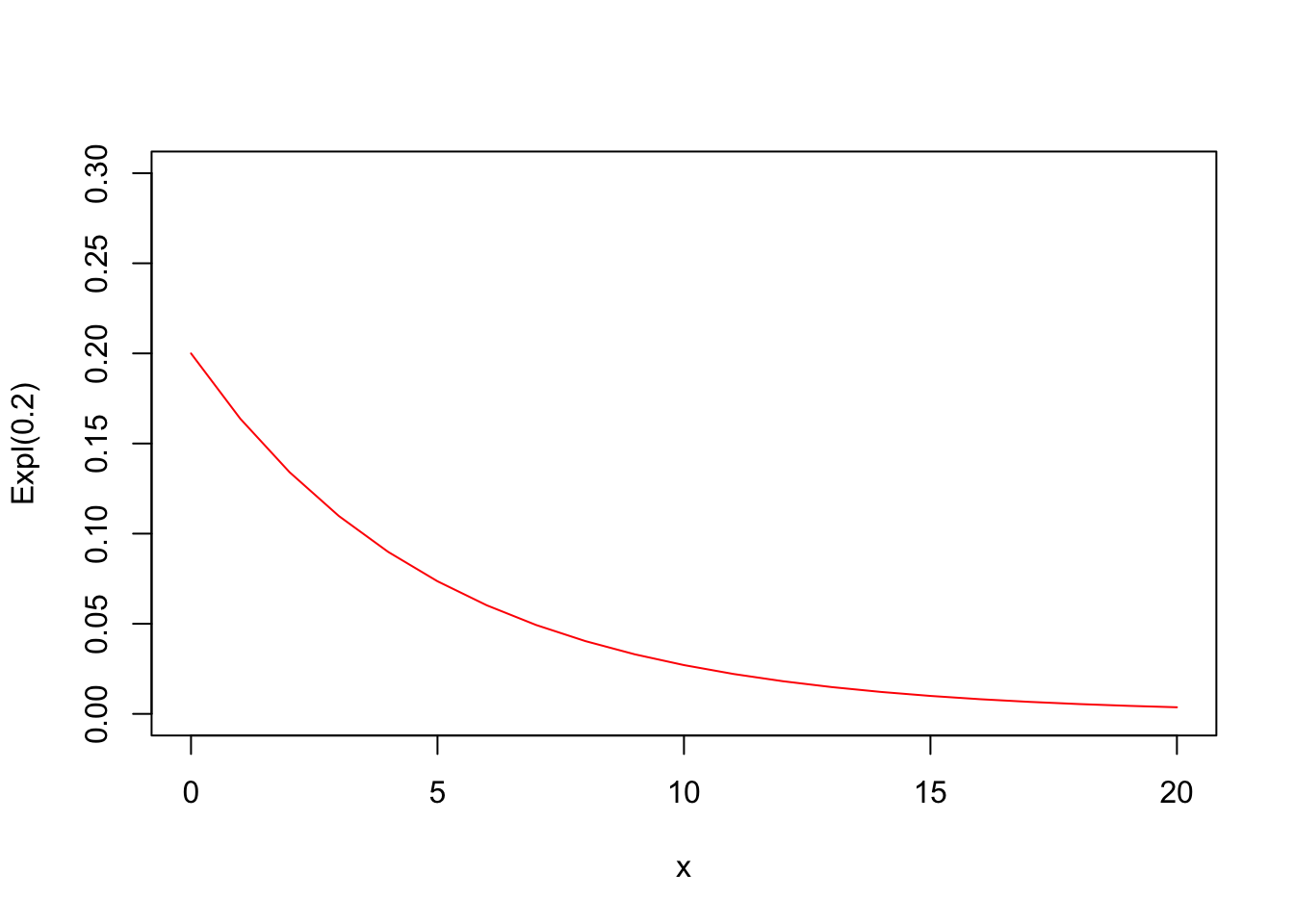
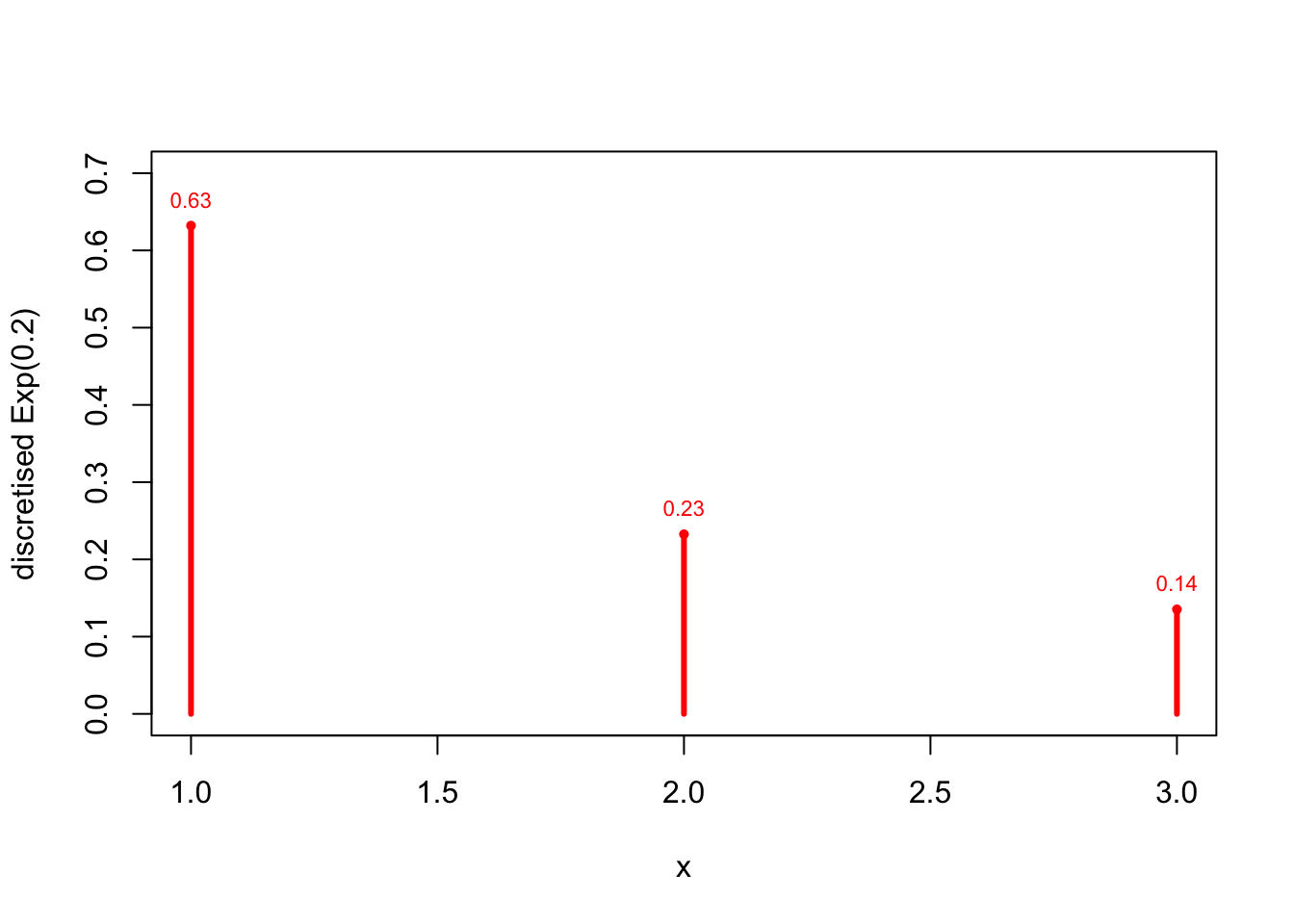
We choose to discretise with 33 groups: 0<X<50<X<5, 5<X<105<X<10 and X>5X>5:
p_1 <- pexp(5, rate=0.2)
p_2 <- pexp(10, rate=0.2) - pexp(5, rate=0.2)
p_3 <- 1 - p_1 - p_2
x <- 1:3
prob <- c(p_1,p_2,p_3)
prob## [1] 0.6321206 0.2325442 0.1353353plot(x=x, y=prob, type ="h", lwd=3, col="red", xlab="x",
ylab="discretised Exp(0.2)", ylim=c(0,0.7))
points(x, prob, pch=16, cex=0.7, col="red")
text(x, prob, pos=3, cex=0.7, col="red",
labels = format(round(prob,2), nsmall=2)
)
This will be the distribution under the null-hypothesis. As we example, we generate a random sample of n=100n=100 from the Exponential(λ=0.2λ=0.2) distribution (so that the null-hypothesis is, in fact, true):
data <- rexp(100, rate=0.2)
data_discretised <- cut(data, breaks=c(0,5,10,50))
obs_counts <- table(data_discretised)
obs_counts## data_discretised
## (0,5] (5,10] (10,50]
## 71 13 16n <- 100
E <- n*prob
E## [1] 63.21206 23.25442 13.53353Q <- sum((obs_counts - E)^2/E)
Q## [1] 5.930866# using chisq.test:
res <- chisq.test(x=obs_counts, p=prob)
res##
## Chi-squared test for given probabilities
##
## data: obs_counts
## X-squared = 5.9309, df = 2, p-value = 0.05154qchisq(0.95, df=2)## [1] 5.991465As Qobs=5.930866≯5.991465Qobs=5.930866≯5.991465, we (correctly) do not reject the null-hypothesis.
1.3 Case 2a: Discrete Distribution with Unknown parameters
- Estimate parameters
- apply Chi-squared test with e≠0e≠0
As an example, we test the null-hypothesis that X∼Poisson(λ)X∼Poisson(λ). We draw a random sample of size n=100n=100 from the Poisson(λ=3λ=3) distribution (so the null-hypothesis is, in fact, true), and calculate the observed frequencies. We use the five groups of case 1a: X=0X=0, X=1X=1, X=2X=2, X=3X=3 and X≥4X≥4:
set.seed(1234)
data <- rpois(100, lambda=3)
data## [1] 1 3 3 3 5 3 0 2 4 3 4 3 2 6 2 5 2 2 1 2 2 2 1 0 2 4 3 5 5 0 3 2 2 3 1 4 2
## [38] 2 8 4 3 3 2 3 2 3 4 3 2 4 1 2 4 3 1 3 3 4 1 5 5 0 2 0 2 4 2 3 1 3 1 5 0 4
## [75] 1 3 2 1 2 4 6 3 1 3 1 5 2 2 1 5 1 5 1 1 1 3 2 0 2 4O_help <- table(data)
O_help## data
## 0 1 2 3 4 5 6 8
## 7 18 26 23 13 10 2 1O <- c(O_help[1:4], sum(O_help[5:8]))
O## 0 1 2 3
## 7 18 26 23 26The probabilities under the null hypothesis and the expected frequencies under the null-hypothesis are:
n <- 100
lambda_hat <- mean(data)
help <- dpois(0:3, lambda=lambda_hat)
prob <- c(help, 1 - sum(help))
prob## [1] 0.07353454 0.19192516 0.25046233 0.21790223 0.26617573E <- n*prob
E## [1] 7.353454 19.192516 25.046233 21.790223 26.617573The observed Q-statistic is equal to:
Q_obs <- sum( (O - E)^2/E )
Q_obs## [1] 0.2088999qchisq(0.95, df=3)## [1] 7.8147281 - pchisq(0.2089, df=3)## [1] 0.9761399#using chisq.test:
chisq.test(O, p=prob)##
## Chi-squared test for given probabilities
##
## data: O
## X-squared = 0.2089, df = 4, p-value = 0.9949As Qobs=0.2088999≱7.814728Qobs=0.2088999≱7.814728, we (correctly) do not reject the null-hypothesis that X∼Poisson(λ)X∼Poisson(λ). The correct p-value is equal to 0.97613990.9761399: the chisq.test command does not take into account that λλ was estimated (as it cannot know this).
1.4 Case 2b: Continuous Distribution with Unknown parameters
- Estimate parameters
- Discretise
- apply Chi-squared test with e≠0e≠0
We use the same example as in case 1b, with null-hypothesis H0:X∼Exp(λ)H0:X∼Exp(λ). We estimate λλ using the maximum likelihood estimator:
ˆλML=1ˉX.^λML=1¯X.
We then discretise using the three groups we used before, calculate Q and compare with qχ2k−1−e0.95qχ2k−1−e0.95 with e=1e=1 in this case:
#estimate lambda using raw data:
set.seed(12345)
raw_data <- rexp(100, rate=0.2)
lambda_hat <- 1/mean(raw_data)
lambda_hat## [1] 0.2000546#calculate probabilities under H0:
p_1 <- pexp(5, rate=lambda_hat)
p_2 <- pexp(10, rate=lambda_hat) - pexp(5, rate=lambda_hat)
p_3 <- 1 - p_1 - p_2
x <- 1:3
prob <- c(p_1,p_2,p_3)
prob## [1] 0.6322210 0.2325176 0.1352614We see that the probabilities under the null-hypothesis have not changed much. We now discretise the data, calculate the frequencies and perform the test:
# discretise the data and calculate counts:
data_discretised <- cut(raw_data, breaks=c(0,5,10,50))
obs_counts <- table(data_discretised)
obs_counts## data_discretised
## (0,5] (5,10] (10,50]
## 66 21 13# chi-squared test:
chisq.test(obs_counts, p=prob)##
## Chi-squared test for given probabilities
##
## data: obs_counts
## X-squared = 0.36059, df = 2, p-value = 0.835# Correct critical value and p-value:
qchisq(0.95, df=1)## [1] 3.8414591 - pchisq(0.36059, df=1)## [1] 0.5481787As Qobs=0.36059≯3.841459Qobs=0.36059≯3.841459, we (correctly) do not reject the null-hypothesis. The correct p-value is 0.54817870.5481787: the chisq.test command does not take into account that we estimated one parameter (as it cannot know this).
2 Bivariate Distributions
The distribution under the null-hypothesis is now a bivariate discrete distribution. For example, somebody could be claiming to know that the population distribution has the following probability mass function:
fX,Y(i,j)=P(X=i,Y=j)=i+j12for i=1,2,3 and j=1,2.fX,Y(i,j)=P(X=i,Y=j)=i+j12for i=1,2,3 and j=1,2.
The random variable XX has r=3r=3 categories and the random variable YY has c=2c=2 categories. We can graph the 66 probabilities of this bivariate population distribution:
We can also simply display the population probabilities in 2-by-3 table (in general this table is rr-by-cc):
| Prob | Y=1Y=1 | Y=2Y=2 | Y=3Y=3 | TotalTotal |
|---|---|---|---|---|
| X=1X=1 | p11=221p11=221 | p12=321p12=321 | p13=421p13=421 | p1∙=921p1∙=921 |
| X=2X=2 | p21=321p21=321 | p22=421p22=421 | p23=521p23=521 | p2∙=1221p2∙=1221 |
| TotalTotal | p∙1=521p∙1=521 | p∙2=721p∙2=721 | p∙3=921p∙3=921 | p∙∙=1p∙∙=1 |
Note that we have introduced notation for the marginal distributions: the marginal probability P(X=1)P(X=1), for example, is denoted by p1∙p1∙:
P(X=1)=3∑j=1P(X=1,Y=j)=3∑j=1p1j≡p1∙P(X=1)=3∑j=1P(X=1,Y=j)=3∑j=1p1j≡p1∙
When we draw a random sample of size n=100n=100 from this population distribution, we obtain (after calculating the frequencies from the raw data):
set.seed(12345)
raw_data <- rmultinom(n=100, size=1, prob=c(2/21,3/21,3/21,4/21,4/21,5/21))
raw_data[,1:10]## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 0 0 0 1 0 0 0 0 0 0
## [2,] 1 1 0 0 0 0 0 0 0 0
## [3,] 0 0 0 0 0 0 1 0 0 0
## [4,] 0 0 0 0 0 0 0 1 1 0
## [5,] 0 0 1 0 0 1 0 0 0 0
## [6,] 0 0 0 0 1 0 0 0 0 1freq <- rowSums(raw_data)
freq## [1] 14 12 16 18 18 22table <- matrix(freq, nrow = 2)
table## [,1] [,2] [,3]
## [1,] 14 16 18
## [2,] 12 18 22Note that when we drew a random sample from the population distribution, we just used a vector of probabilities (not a matrix of probabilities). There is no real difference between a bivariate distribution with 66 probabilities pijpij and a univariate distribution with 66 probabilities pipi. We only use the two subscripts ii and jj because it is more intuitive given that the data is organised that way. We can introduce notation for row-totals and column-totals as follows:
| Freq | Y=1Y=1 | Y=2Y=2 | Y=3Y=3 | TotalTotal |
|---|---|---|---|---|
| X=1X=1 | O11=14O11=14 | O12=16O12=16 | O13=18O13=18 | O1∙=48O1∙=48 |
| X=2X=2 | O21=12O21=12 | O22=18O22=18 | O23=22O23=22 | O2∙=52O2∙=52 |
| TotalTotal | O∙1=26O∙1=26 | O∙2=34O∙2=34 | O∙3=40O∙3=40 | n=O∙∙=100n=O∙∙=100 |
With the notation for bivariate distributions (and observed frequencies) established, we can now formulate the method to test the null-hypothesis that the population distribution is some pre-specified bivariate Multinomial distribution:
Chi-squared Test: The Method (Bivariate)
- step 1: specify H0H0, possibly after first estimating ee parameters (and discretising if XX is continuous): a Multinomial distribution with k=rck=rc groups.
- step 2: Calculate Eij=npijEij=npij, the expected frequencies if H0H0 is true, for i=1,…,ri=1,…,r and j=1,…,cj=1,…,c. For each (i,j)(i,j), we need Eij≥5Eij≥5.
- step 3: Calculate Qobs=∑ri=1∑cj=1(Oij−Eij)2EijQobs=∑ri=1∑cj=1(Oij−Eij)2Eij and reject H0H0 if Qobs>qχ2rc−1−e0.95Qobs>qχ2rc−1−e0.95.
2.1 Case 3a: Known Bivariate Discrete Distributions
- apply the Chi-squared test directly with e=0e=0
- Make sure that that Eij≥5Eij≥5 for i=1,2,…,ri=1,2,…,r and j=1,2,…,cj=1,2,…,c.
In the example above, the null-hypothesis was that the population distribution was a bivariate discrete distribution with known probabilities pijpij. This example is hence of case 3a. We can simply calculate the chi-squared statistic QQ: there is no need to estimate parameters and there is also no need to discretise.
# Calculate Q ourselves:
n <- 100
prob=c(2/21,3/21,3/21,4/21,4/21,5/21)
sum((freq-n*prob)^2/(n*prob))## [1] 2.928qchisq(0.95, df=5)## [1] 11.0705# Check result using chisq.test:
chisq.test(x=freq, p=prob)##
## Chi-squared test for given probabilities
##
## data: freq
## X-squared = 2.928, df = 5, p-value = 0.7111As Qobs=2.928≯11.07Qobs=2.928≯11.07, we (correctly) do not reject the null-hypothesis. The p-value is 0.7111.
2.2 Case 3b: Known Bivariate Continuous Distributions
- Discretise
- apply Chi-squared test with e=0e=0
The most commonly used continuous bivariate distribution is the bivariate Normal distribution. Its marginal distributions are univariate Normals. The random variables XX and YY can be correlated or uncorrelated (in which case they are independent). In the graph below, the marginal distributions are taken to be standard-normal. In the upper graphs, XX and YY have Cov[X,Y]=0Cov[X,Y]=0. The lower graphs show the bivariate density with Cov[X,Y]=Corr[X,Y]=0.5Cov[X,Y]=Corr[X,Y]=0.5. The graphs on the right show the distributions using isoquants (a helicopter-view), which is often easier to interpret.
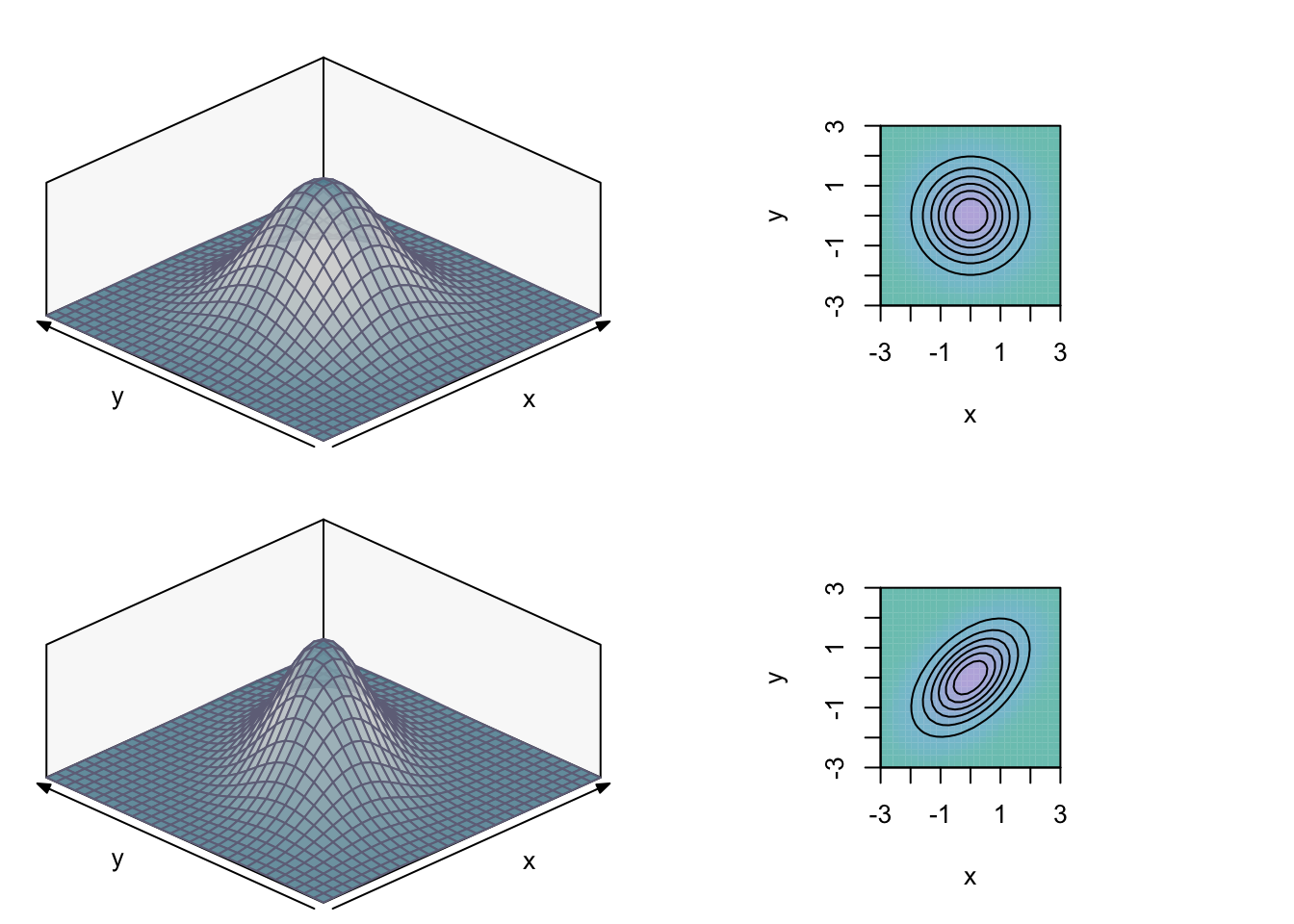
We will take the uncorrelated bivariate standard Normal distribution as our null-hypothesis. As both XX and YY take most values between −2−2 and 22, we discretise the bivariate continuous distribution into 1616 areas, with both XX and YY divided by the intervals (−∞,−1)(−∞,−1), (−1,0)(−1,0), (0,1)(0,1) and (1,∞)(1,∞). Note that, for bivariate distributions,
P(a1≤X≤a2,b1≤Y≤b2)=FX,Y(a2,b2)−FX,Y(a1,b2)−FX,Y(a2,b1)+FX,Y(a1,b1).
The pbivnorm command from the pbivnorm package can be used to calculate the values of the cdf of bivariate Normal distributions:
library(pbivnorm)
#upper-left area
p_11 <- pbivnorm(x=-1, y=10, rho=0) - pbivnorm(x=-10, y=10, rho=0) -
pbivnorm(x=-1, y=1, rho=0) + pbivnorm(x=-10, y=-10, rho=0)
p_14 <- p_11
p_41 <- p_11
p_44 <- p_11
p_12 <- pbivnorm(x=0, y=10, rho=0) - pbivnorm(x=-1, y=10, rho=0) -
pbivnorm(x=0, y=1, rho=0) + pbivnorm(x=-1, y=1, rho=0)
p_13 <- p_12
p_42 <- p_12
p_43 <- p_12
p_21 <- pbivnorm(x=-1, y=1, rho=0) - pbivnorm(x=-10, y=1, rho=0) -
pbivnorm(x=-1, y=0, rho=0) + pbivnorm(x=-10, y=0, rho=0)
p_31 <- p_21
p_24 <- p_21
p_34 <- p_21
p_22 <- pbivnorm(x=0, y=1, rho=0) - pbivnorm(x=-1, y=1, rho=0) -
pbivnorm(x=0, y=0, rho=0) + pbivnorm(x=-1, y=0, rho=0)
p_23 <- p_22
p_32 <- p_22
p_33 <- p_22
c(p_11,p_12,p_21,p_22)## [1] 0.02517149 0.05415614 0.05415614 0.11651624prob <- c(p_11, p_21, p_31, p_41,
p_12, p_22, p_32, p_42,
p_13, p_23, p_33, p_43,
p_14, p_24, p_34, p_44)
sum(prob)## [1] 1We can now plot the discretised version of our bivariate standard-normal distribution:
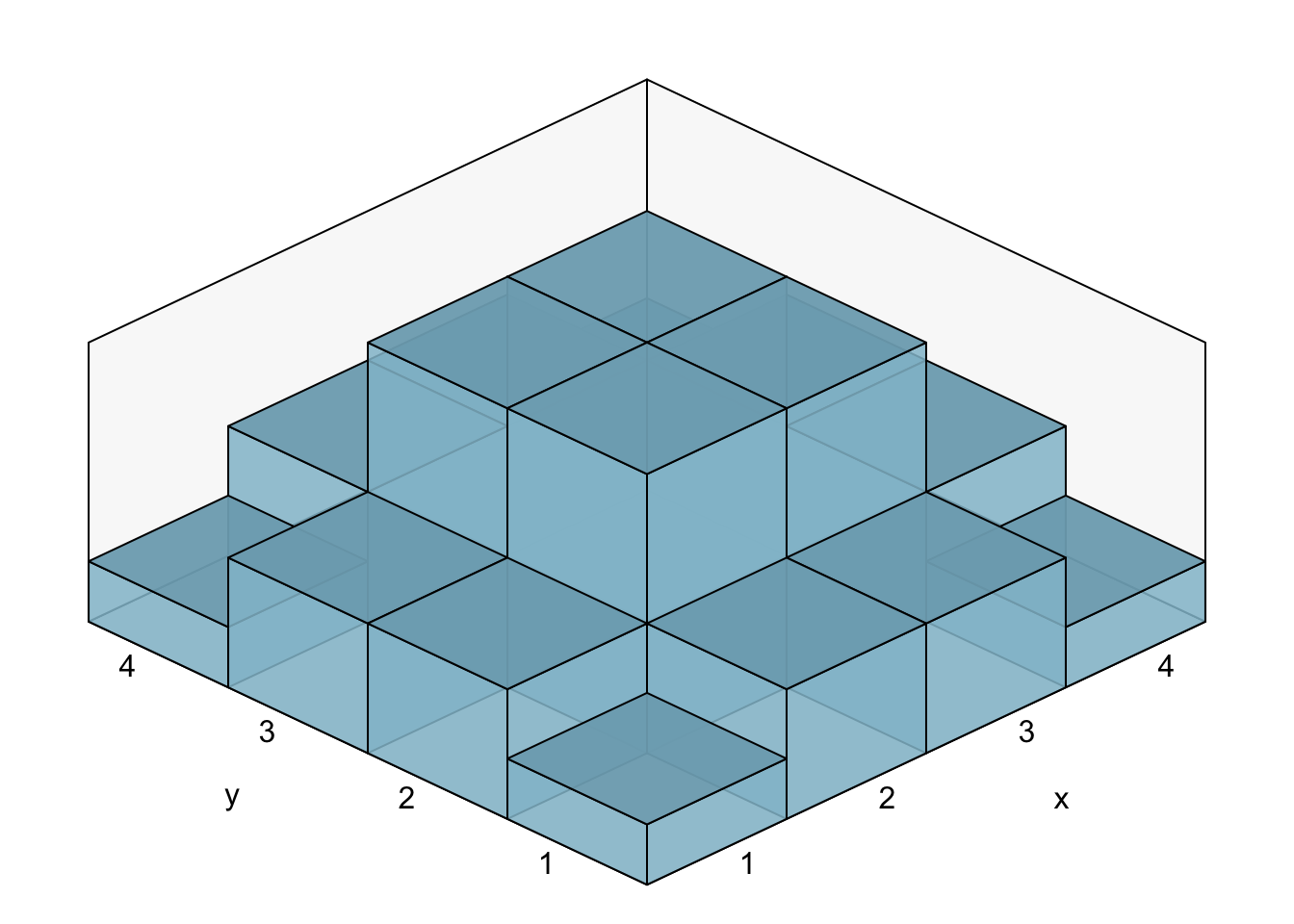
We take this distribution as our null-hypothesis. We generate some data and perform the Chi-square-test:
set.seed(12345)
x <- rnorm(1000)
y <- rnorm(1000)
x_discrete <- cut(x,breaks=c(-10,-1:1, 10))
y_discrete <- cut(y,breaks=c(-10,-1:1, 10))
data <- table(x_discrete, y_discrete)
data## y_discrete
## x_discrete (-10,-1] (-1,0] (0,1] (1,10]
## (-10,-1] 32 44 52 21
## (-1,0] 55 110 111 53
## (0,1] 53 138 115 68
## (1,10] 21 55 48 24c(data)## [1] 32 55 53 21 44 110 138 55 52 111 115 48 21 53 68 24chisq.test(c(data), p= prob)##
## Chi-squared test for given probabilities
##
## data: c(data)
## X-squared = 14.201, df = 15, p-value = 0.5103qchisq(0.95, df=15)## [1] 24.99579As Qobs=14.201≯24.996, we (correctly) do not reject the null-hypothesis.
2.3 Case 4a: Bivariate Discrete Distributions With Unknown Parameters
- Estimate parameters
- apply Chi-squared test with e≠0
Instead of describing an example of this case, we will go deeper into the very important test for independence of two discrete random variables. This test turns out to belong to this case 4a (which in itself is almost equal to case 2a).
Testing for Independence in A Contingency Table
An important application of case 4a is testing if two discrete random variables are independent. Two discrete random variables X (taking the values 1,…,r) and Y (taking the values j=1,…,c) are called independent if
P(X=i,Y=j)=P(X=i)P(Y=j) for all i=1,…,r and j=1,…c. If all the marginal probabilities P(X=i) and P(Y=j) were known, we could formulate the null-hypothesis: under the null-hypothesis we would have a Multinomial distribution with rc known probabilities pij for i=1,…,r and j=1,…c.
These marginal probabilities can, however, easily be estimated using the row-totals Oi∙ and column-totals O∙j of our observed frequency table:
^P(X=i)=Oi∙n for i=1,…,r.^P(Y=j)=O∙jn for j=1,…,c.
As ∑ri=1P(X=i)=1, we need only estimate P(X=i) for i=1,…,r−1. As ∑cj=1P(Y=j)=1 as well, we need only estimate P(Y=j) for j=1,…,c−1. Therefore, in total, we need to estimate e=(r−1)+(c−1) parameters.
We now have estimates of the probabilities of our bivariate discrete Multinomial distribution if the null-hypothesis is true. From these, we can obtain the expected frequencies:
Eij=n^P(X=i,Y=j)=H0n^P(X=i)^P(Y=j)=nOi∙nO∙jn=Oi∙O∙jn.
We are now ready to compute Qobs.
Note that the test for independence is simply a special case of case 2a. The degrees of freedom of the Chi-squared test equal rc−1−(r−1)−(c−1), which can be written as (r−1)(c−1):
rc−1−(r−1)−(c−1)=rc−1−r+1−c+1=rc−r−c+1=(r−1)(c−1).
Under the null-hypothesis, we therefore have
Q=r∑i=1c∑i=1(Oij−Eij)2Eijapprox∼H0χ2(r−1)(c−1).
We now have the following method to test for independence of two discrete random variables:
Chi-squared Test: Test for Independence
- step 1: H0: X and Y are independent. The random variables X and Y are both discrete (X has r groups and Y has c groups).
- step 2: Calculate Eij=Oi∙O∙jn, the expected frequencies if H0 is true, for i=1,…,r and j=1,…,c. For each (i,j), we need Eij≥5.
- step 3: Calculate Qobs=∑ri=1∑cj=1(Oij−Eij)2Eij and reject H0 if Qobs>qχ2(r−1)(c−1)0.95.
As an example, let’s test if smoking habit is independent of exercising, using the chisq.test command:
library(MASS) # load the MASS package
head(survey[, c("Exer", "Smoke")]) # first 6 observations of raw data## Exer Smoke
## 1 Some Never
## 2 None Regul
## 3 None Occas
## 4 None Never
## 5 Some Never
## 6 Some Neverfreq <- table(survey$Smoke, survey$Exer)
freq # the contingency table (or: frequency table)##
## Freq None Some
## Heavy 7 1 3
## Never 87 18 84
## Occas 12 3 4
## Regul 9 1 7res <- chisq.test(freq)## Warning in chisq.test(freq): Chi-squared approximation may be incorrectres##
## Pearson's Chi-squared test
##
## data: freq
## X-squared = 5.4885, df = 6, p-value = 0.4828res$expected##
## Freq None Some
## Heavy 5.360169 1.072034 4.567797
## Never 92.097458 18.419492 78.483051
## Occas 9.258475 1.851695 7.889831
## Regul 8.283898 1.656780 7.059322The warning message in the output occurs because not all expected frequencies are larger or equal than 5. We combine the None and Some columns to deal with this:
freq_new = cbind(freq[,"Freq"], freq[,"None"] + freq[,"Some"])
freq_new## [,1] [,2]
## Heavy 7 4
## Never 87 102
## Occas 12 7
## Regul 9 8res2 <- chisq.test(freq_new)
res2##
## Pearson's Chi-squared test
##
## data: freq_new
## X-squared = 3.2328, df = 3, p-value = 0.3571res2$expected## [,1] [,2]
## Heavy 5.360169 5.639831
## Never 92.097458 96.902542
## Occas 9.258475 9.741525
## Regul 8.283898 8.716102As all Eij≥5, we do not get a warning message this time. As the p-value is larger than 5%, we do not reject the null-hypothesis that Smoke and Exer are independent. Note that, as an example, E11 can be calculated as follows:
colSums(freq_new)## [1] 115 121rowSums(freq_new)## Heavy Never Occas Regul
## 11 189 19 17E11=O1∙O∙1n=11×115236=5.360169.
2.4 Case 4b: Bivariate Continuous Distributions With Unknown Parameters
- Estimate parameters
- Discretise
- apply Chi-squared test with e≠0
Suppose that, in the example of case 3b, we would not have known the values of the two means, the two variances and the covariance. We can still use the Chi-squared test, using the estimated parameters. As e=5 in this case, the only change would be the critical value: instead of df=15, we would now have df=16−1−5=10. The parameters are easily estimated
n <- 1000
raw_data <- cbind(x,y)
colMeans(raw_data)## x y
## 0.04619816 -0.03039248#maximum likelihood estimator is UNadjusted sample variance/covariance:
((n-1)/n)*var(raw_data)## x y
## x 0.99649932 0.03901121
## y 0.03901121 1.01575949We would proceed to test the null-hypothesis that (X,Y) has a bivariate Normal distribution with μX=0.04619816, μY=−0.03039248, Var[X]=0.99649932, Var[Y]=1.01575949 and Cov[X,Y]=0.03901121. As this bivariate Normal distribution is almost equal to the bivariate standard-normal, we do not expect the test to give a different result. In particular, we expect that the value of Qobs will again be somewhere between 13 and 15 (it was equal to 14.201 in the example of case 3b). The critical value can be quite different with df=10:
qchisq(0.95, df=15)## [1] 24.99579qchisq(0.95, df=10)## [1] 18.30704The null-hypothesis would probably again not be rejected.