3. Repeated Sampling Distributions
- 1 Population Distribution versus Repeated Sampling Distribution
- 2 Questions About The Mean (or Proportion) of a Single Population
- 3 Questions About The Means (or Proportions) of Two Populations
- 4 Questions About The Variance of A Single Population
- 5 Questions About The Variances of Two Populations
- 6 Questions about the Maximum or Minimum (Order Statistics)
We will discuss some results that we will need in later chapters. Most of these results are of the following type:
Suppose that the population distribution (the distribution of the random variable \(X\)) is known to belong to some known family of distributions, and that we have at our disposal a random sample \(X_1,\ldots,X_n\) from that distribution. Then, the distribution of some function \(T(X_1,\ldots,X_n)\) of the random sample has a certain distribution.
Examples of functions of a random sample are:
- \(T(X_1,\ldots,X_n) = \sum_{i=1}^n X_i\)
- \(T(X_1,\ldots,X_n) = \frac{1}{n}\sum_{i=1}^n X_i=\bar{X}\)
- \(T(X_1,\ldots,X_n) = \sum_{i=1}^n \left( X_i-\bar{X} \right)^2=(n-1)S^{\prime 2}\)
Estimators (chapters 3 and 7), confidence intervals (chapter 4) and test-statistics (chapters 5 and 6) are examples of functions of a random sample. An example of the type of results that we will be discussing (and using) in this chapter is:
If \(X \sim N(\mu,\sigma^2)\) then
\(T(X_1,\ldots,X_n)=\bar{X} \sim N(\mu, \frac{\sigma^2}{n}).\)
Another example:
If \(X \sim Poisson(\lambda)\) then \(T(X_1,\ldots,X_n)=\sum_{i=1}^n X_i \sim Poisson(n\lambda).\)
1 Population Distribution versus Repeated Sampling Distribution
What is inferential statistics all about?
The goal of inferential statistics is:
To give a credible answer to an interesting question using data. Moreover, the uncertainty that is due to sampling should be quantified.
Let’s look at an example: consider the population distribution of incomes of people living in Portugal. For the moment, we will not assume anything about this unknown distribution. What we want is to estimate the expected value (or: mean \(\mu = E[X]\)) of this distribution. We decide to use the sample average \(\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i\) as an estimator for \(E[X]\). Using a sample of size \(n=3\), we obtain \(\bar{X}=6\). How accurate is this number as an estimate of \(\mu\)?
The reason why we have to ask ourselves this question is that we know that if we were to draw another random sample of size 3 we would obtain a different value for the sample average and hence a different estimate for the unknown value of \(\mu\). Will this estimate be close to \(6\) or completely different? As it stands, we do not know. How can we quantify this uncertainty due to sampling? We will use the so-called repeated sampling distribution (RSD) of \(\bar{X}\):
Imagine that we would obtain 10 million (or even better: infinitely many) random samples of size \(n=3\) from the income distribution. For each of those random samples, we could then obtain the sample average. The distribution of sample averages (we can plot this distribution using a histogram) is called the repeated sampling distribution of the sample average (\(RSD(\bar{X}\))). This distribution is useful for the following reason: our observed sample average \(\bar{X}=6\) can be considered a (single) draw from this distribution, i.e. we have observed a sample of size 1 from \(RSD(\bar{X})\). If the variance of \(RSD(\bar{X})\) is small, we would know that if we were to draw a second random sample of size 3, the value of the sample average that we would obtain (also a sample of size 1 from \(RSD(\bar{X})\)) will be close to 6. This means that the sampling error can be considered small if \(\mathbf{Var[RSD(\bar{X})]}\) is small!
The following animation shows what \(RSD(\bar{X})\) would look like when the population distribution is discrete uniform (which takes values between 0 and 9 with equal probability) and \(n=3\). To keep the animation short, we only draw 100 repeated samples, not 10 million:
The problem that remains is to obtain the repeated sampling distribution of \(\bar{X}\). This seems impossible, as we only have access to a single sample of size 3 and hence only have access to a single sample average (equal to 6 in our case). Fortunately, however, we can use mathematics to obtain the mean and variance of \(RSD(\bar{X})\). The mathematics required is not very complicated: three rules for the mean of a random variable and three rules for the variance of a random variable.
Rules for the mean and variance of a random variable \(X\):
Let \(c\) denote a constant (not random).
\[ \begin{align} \mathbf{E1:} & \; E \left[ c \right] = c \\ \mathbf{E2:} & \; E \left[ c X \right] = c E \left[ X \right] \\ \mathbf{E3:} & \; E \left[ \sum_{i=1}^n X_i \right] = \sum_{i=1}^n E \left[ X_i \right] \\ \mathbf{V1:} & \; Var \left[ c \right] = 0 \\ \mathbf{V2:} & \; Var \left[ c X \right] = c^2 Var \left[ X \right] \\ \mathbf{V3:} & \; Var \left[ X_1 \mp X_2 \right] = Var[X_1] + Var[X_2] \mp Cov[X_1,X_2] \end{align} \]Using the rules, we obtain:
The mean and variance of \(RSD(\bar{X})\) (for any distribution of \(X\)):
\[ \begin{align} E \left[ \frac{1}{n} \sum_{i=1}^n X_i \right] &\overset{E3}{=} \sum_{i=1}^n E[\frac{1}{n} X_i] \overset{E2}{=} \sum_{i=1}^n \frac{1}{n} E[X_i] \overset{E[X_i]=E[X]}{=} E[X]. \\ Var \left[ \frac{1}{n} \sum_{i=1}^n X_i \right] &\overset{V3}{=} \sum_{i=1}^n Var[\frac{1}{n} X_i] \overset{V2}{=} \sum_{i=1}^n \frac{1}{n^2} Var[X_i] \overset{Var[X_i]=Var[X]}{=} \frac{Var[X]}{n}. \end{align} \]The first result shows that the sample average is an unbiased estimator of the population mean: in repeated samples, the sample average would on average in repeated samples estimate the value of \(E[X]\) correctly. This means that \(\bar{X}\) does not systematically over-estimate of under-estimate \(E[X]\) in repeated samples.
The second result states that the variance of the repeated sampling distribution of the sampling average equals the variance of the population distribution devided by \(n\), the sample size.
- Note that we cannot simply use the sample variance of \(RSD(\bar{X})\) to estimate \(Var[RSD(\bar{X})]\), as we only have a sample of size 1 from \(RSD(\bar{X})\). We can, however, estimate \(Var[X]\), the variance of the population distribution, using the sample variance: we have a sample of size \(n\) from the population distribution. This makes the second result very useful: we can estimate the variance of a distribution from which we have only a sample of size 1 because the second results relates this variance to the variance of a distribution from which we have a sample of size \(n\).
- Note also that we did not make any assumptions about the population distribution (e.g. we did not assume that it is a Normal distribution). Both results are true for any population distribution. We will see later that if we were to assume that the population distribution is a Normal distribution, \(RSD(\bar{X})\) will also be a Normal distribution (with mean \(E[X]\) and variance \(\frac{Var[X]}{n}\), of course).
We have been working on an example where the question was: what is the mean of a random variable \(X\) (more specifically: what is the mean income of a Portuguese person)? Other questions could be about the variance of a random variable \(X\).
Note that the variance of the population distribution can be estimated by the sample variance
\[ S^2 = \frac{1}{n}\sum_{i=1}^n (X_i - \bar{X})^2, \]
or the adjusted sample variance
\[ S^{\prime 2} = \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2. \]
The adjusted sample variance is better because it is an unbiased estimator of \(\sigma^2\):
\[ E[RSD(S^{\prime 2})] = E[S^{\prime 2}]=\sigma^2. \]
This implies that \(S^2\) is a biased estimator of \(\sigma^2\):
\[ E[RSD(S^2)]=E[S^2]=E\left[ \frac{n-1}{n}S^{\prime 2}\right]=\frac{n-1}{n}E[S^{\prime 2}]=\frac{n-1}{n}\sigma^2 \neq \sigma^2. \]
Sometimes we are more interested in the difference between the means/variances of two different populations (for instance Portugal and England). The answer to all the questions mentioned above will depend on what we assume about the population distribution (e.g. is it Normal or Exponential or Poisson?). In what follows, we will discuss several example situations and discuss the results that are required to answer (potentially interesting) questions in those situations.
Most of these questions can be answered by knowing something about the RSD of the sample average (sometimes it is easier to use the RSD of \(\sum_{i=1}^n X_i\)) or the RSD of the sample variance \(S^{\prime 2}= \frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2\), given what is assumed about the population distribution.
In total, we will accumulate 15 results.
2 Questions About The Mean (or Proportion) of a Single Population
The 10 most important RSD-results for questions about the mean will turn out to be:
- linear combinations of Normals are Normal. This implies that \(X \sim N(\mu,\sigma^2) \implies \bar{X} \sim N(\mu, \frac{\sigma^2}{n})\)
- Central Limit Theorem (CLT): sample average is approximately Normal (regardless of the distribution of X)
- standardise Normal with known variance: standard-normal distribution
- standardise Normal with estimated variance: t distribution
- sum of Bernoulli(\(p\)) is Binomial(\(n,p\))
- Binomial(\(n,p\)) with large \(n\) and small \(p\) is approximately Poisson(\(\lambda=np\))
- sum of Poisson(\(\lambda_i\)) is Poisson(\(\sum_{i=1}^n \lambda_i\))
- constant (c) times Exponential(\(\lambda\)) is Exponential(\(\frac{\lambda}{c}\))
- sum of Exponential(\(\lambda\)) is Gamma(\(n,\lambda\))
- \(2\lambda\) times Gamma(\(n,\lambda\)) is Chi-squared(\(2n\))
2.1 Example 1: \(X \sim N(\mu,\sigma^2)\)
We are considering the situation where we are willing to assume that the population distribution is a member of the family of Normal distributions. We are interested in finding the RSD of the sample average. As the sample average will turn out to be a linear combination of Normals, we need the following result:
Theorem 1 - Linear Combinations of Normals are Normal: Suppose that the population distribution is a Normal distribution with mean \(E[X]=\mu\) and variance \(Var[X]=\sigma^2\). In other words, \(X \sim N(\mu,\sigma^2)\).
Suppose that we have a random sample of size \(n\) from this population distribution: \(X_1,X_2,\ldots,X_n\) iid (independent and identically distributed). Then, any linear combinations of \(X_1,X_2,\ldots,X_n\) also has a Normal distribution. That is:
\[ X \sim N(\mu,\sigma^2) \implies c_1 X_1 + c_2 X_2 + \cdots + c_n X_n \sim N(\mu \sum_{i=1}^n c_i, \sigma^2 \sum_{i=1}^n c_i^2).\]Note: The mean and the variance of the Normal distribution follow directly from the rules for the mean (E1,E2,E3) and the rules for the variance (V1,V2,V3):
\[ \begin{align} E \left[ \sum_{i=1}^n c_i X_i \right] &\overset{E3}{=} \sum_{i=1}^n E[c_i X_i] \overset{E2}{=} \sum_{i=1}^n c_i E[X_i] \overset{E[X_i]=\mu}{=} \mu \sum_{i=1}^n c_i. \\ Var \left[ \sum_{i=1}^n c_i X_i \right] &\overset{V3}{=} \sum_{i=1}^n Var[c_i X_i] \overset{V2}{=} \sum_{i=1}^n c_i^2 Var[X_i] \overset{Var[X_i]=\sigma^2}{=} \sigma^2 \sum_{i=1}^n c_i^2. \end{align} \]The exact RSD of the sample average: if we take \(c_i=\frac{1}{n} \; \; i=1,2,\ldots,n\) in Theorem 1, we obtain the important result that the repeated sampling distribution of the sample average is a Normal distribution when sampling from the Normal distribution:
\[ X \sim N(\mu,\sigma^2) \implies \frac{1}{n}\sum_{i=1}^n X_i \sim N(\mu, \frac{\sigma^2}{n}).\]
2.1.1 Aproximation using CLT
In cases where the assumption that the populaton distribution is Normal is not credible, it turns out that (if the sample is large) the RSD of \(\bar{X}\) is still well-approximated by a Normal distribution. This is very useful because we are often hesitant to assume something about the population distribution.
Theorem 2 - The Central Limit Theorem (CLT): The RSD of \(\bar{X}\) is approximately Normal if the sample is large. Suppose that the population distribution is not a Normal distribution, or that we have no information that allows us to pinpoint some family of distributions from which the population distribution is a member. In other words, for example \(X \sim Bernoulli(p)\) or \(X \sim \; ?\)
Suppose that we have a random sample of size \(n\) from the population distribution: \(X_1,X_2,\ldots,X_n\) iid. Then, the Repeated Sampling Distribution of the sample average \(\bar{X}\) is approximately Normal. The approximation becomes more precise the larger the sample is. That is (informally):
\[ X \sim \: \: ? \implies \bar{X} \overset{approx}{\sim} N \left( \mu, \frac{\sigma^2}{n} \right).\]
The formally correct statement is:
\[ X \sim \: \: ? \implies \sqrt{n}(\bar{X}-\mu) \overset{d}{\rightarrow}N(0,\sigma^2),\]
where \(\overset{d}{\rightarrow}\) stands for “converges in distribution to”.Note that the informal and formal ways to state the central limit theorem are essentially the same:
- if \(\sqrt{n}(\bar{X}-\mu) \sim N(0,\sigma^2)\) then \((\bar{X}-\mu) \sim N(0,\frac{\sigma^2}{n})\) by V2 and Theorem 1.
- if \((\bar{X}-\mu) \sim N(0,\frac{\sigma^2}{n})\) then \(\bar{X} \sim N(\mu,\frac{\sigma^2}{n})\). Adding a constant \(\mu\) to each repeated sampling realisation of the random variable \(\bar{X}-\mu\) shifts the mean and does not change the variance.
The formal way of stating the CLT uses the notation \(\overset{d}{\rightarrow}\), which stands for “converges in distribution to”. It means that if we let \(n\rightarrow \infty\), the distribution of the random variable \(\sqrt{n}(\bar{X}-\mu)\) is exactly \(N(\mu, \frac{\sigma^2}{n})\). We cannot let \(n\rightarrow \infty\) in the informal statement because the sample size \(n\) appears on the right-hand side. The informal statement is not an exact statement.
We can illustrate the Central Limit Theorem by repeating the RSD-animation with a larger sample-size: we take 10000 random samples of size \(100\) (instead of \(3\)) from the Uniform(\(\{0,1,\ldots,9\}\)) distribution. We have no theorem that states what the exact RSD of \(\bar{X}\) should be. The CLT, however, does predict that \(RSD(\bar{X})\) approximates a Normal distribution:
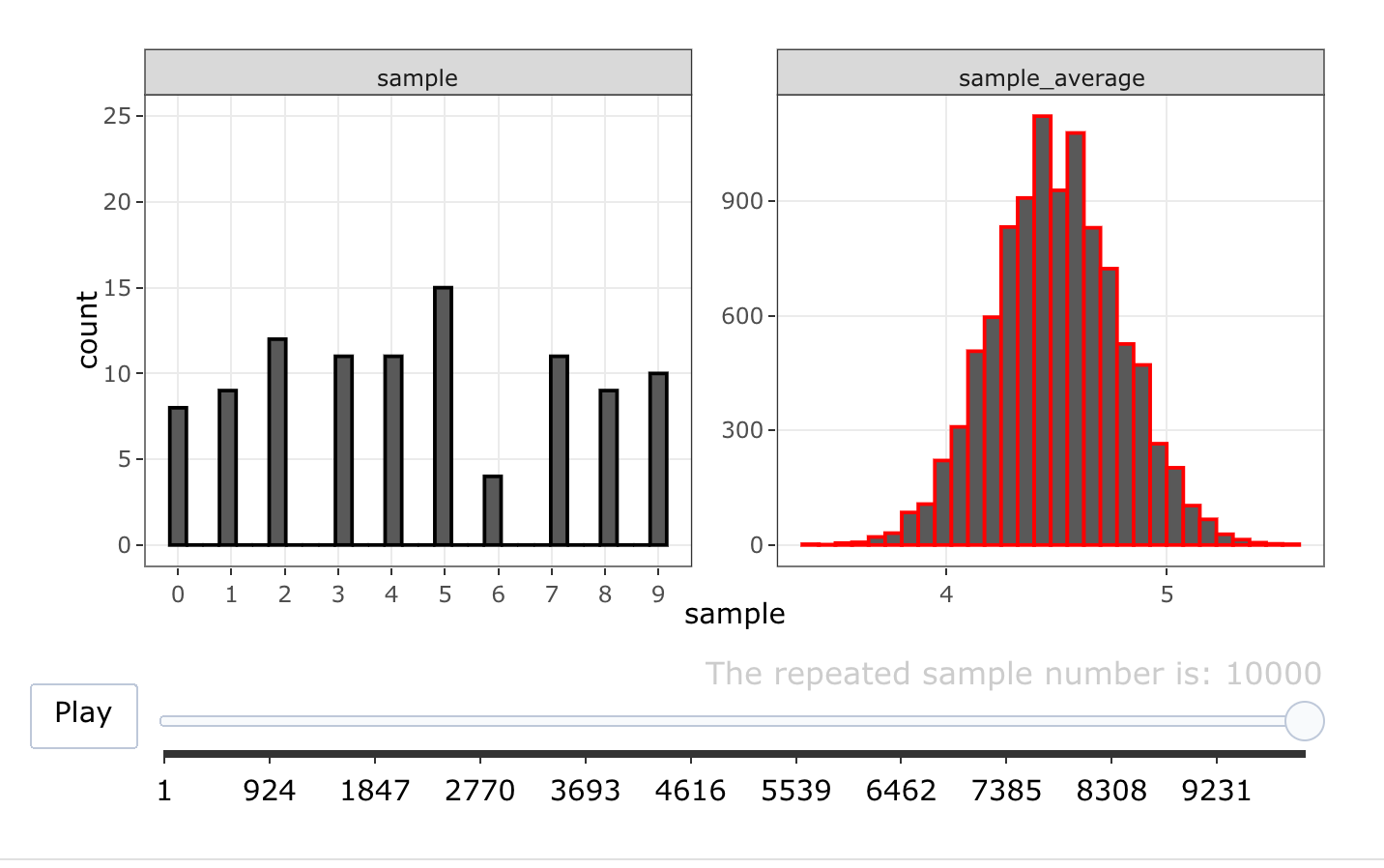
It seems that \(n=100\) is sufficiently large for the RSD of \(\bar{X}\) to be well approximated by a Normal distribution. Moreover, the variance of the RSD is indeed about equal to \(\frac{Var[X]}{n}=\frac{9^2/12}{100}=0.07\): the emprical rule implies that about \(95\%\) of the probability lies in a range of width \(4*\sqrt{0.07}=1.1\).
2.1.2 Standardising A Normal
Although R allows us to calculate probabilities for Normal random variables with any value of \(\mu\) and \(\sigma^2\), if we have to rely on the statistical tables (that only contains the standard-normal distribution) we need to standardise.
Theorem 3 - Standardising A Normal: Suppose that \(X \sim N(\mu,\sigma^2)\).
We can transform the distribution of \(X\) into a standard-Normal by standardising:
\[ X \sim N(\mu,\sigma^2) \implies \frac{X - \mu}{\sqrt{\sigma^2}} \sim N(0,1).\]
If we standardise using the (adjusted) sample variance \(S^{\prime 2}\), we obtain a t-distribution:
\[ X \sim N(\mu,\sigma^2) \implies \frac{X - \mu}{\sqrt{S^{\prime 2}}} \sim t_{n-1}.\]We can use these standardisation results for any Normally distributed random variable:
Note: if we start with \(\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\) (instead of \(X \sim N(\mu, \sigma^2\))) we obtain
\[ \bar{X} \sim N(\mu,\frac{\sigma^2}{n}) \implies \frac{\bar{X} - \mu}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0,1)\] and \[ \bar{X} \sim N(\mu,\frac{\sigma^2}{n}) \implies \frac{\bar{X} - \mu}{\sqrt{\frac{ S^{\prime 2} }{n}}} \sim t_{n-1}.\]
Note: if we start with \(X \sim ?\), we use the CLT: \[ X \sim ? \implies \bar{X} \overset{approx}{\sim} N(\mu,\frac{\sigma^2}{n}) \implies \frac{\bar{X} - \mu}{\sqrt{\frac{ S^{\prime 2} }{n}}} \overset{approx}{\sim} N(0,1).\]2.2 Example 2: \(X \sim Poisson(\lambda)\)
We are considering the situation where we are willing to assume that the population distribution is a member of the family of Poisson distributions. We are interested in finding the RSD of the sample average. Note, however, that we can answer any question about the RSD of the sample average by using the RSD of \(\sum_{i=1}^n X_i\). For instance,
\[ P(\bar{X}<3) = P \left( \sum_{i=1}^n X_i < 3n \right).\] For the Poisson distribution, it turns out that we can formulate the main result more easily using the RSD of \(\sum_{i=1}^n X_i\):
Theorem 4 - Sums of Poissons are Poisson:
Suppose that \(X_1 \sim Poisson(\lambda_1), X_2 \sim Poisson(\lambda_2), \ldots , X_n \sim Poisson(\lambda_n)\),
2.2.1 Aproximation using CLT
If \(X \sim Poisson(\lambda)\), we know that \(E[X]=Var[X]=\lambda\). The central limit theorem then states that \[\bar{X} \overset{approx}{\sim} N(\lambda, \frac{\lambda}{n}).\] This implies that \[\sum_{i=1}^n X_i \overset{approx}{\sim} N(n\lambda, n\lambda).\]
For example, if \(\lambda=1\) and \(n=10\), the exact RSD of \(\sum_{i=1}^n X_i\) is \(Poisson(10)\) and the approximate RSD is \(N(10, 10)\). If we look at the animation for Poisson distributions in the chapter on population distributions, we can see that the \(Poisson(10)\) distribution looks quite similar to the \(N(10,10)\) distribution.
If we want to use the approximate RSD to calculate a probability, we use a continuity correction, as we are approximating a discrete distribution by a continuous distribution. For instance, to approximate the probability that the sum equals 5:
\[\begin{align} P(\sum_{i=1}^n X_i = 5) &= P(Poisson(10)=5) \\ &\overset{approx}{=} P(4.5 < N(10,10) < 5.5) \\ &= \Phi \left( \frac{5.5 - 10}{\sqrt{10}} \right) - \Phi \left( \frac{4.5 - 10}{\sqrt{10}} \right). \end{align}\]
# CLT approximation:
pnorm((5.5-10)/sqrt(10)) - pnorm((4.5-10)/sqrt(10))## [1] 0.0363693# Exact:
dpois(5, lambda=10)## [1] 0.037833272.3 Example 3: \(X \sim Exp(\lambda)\)
We are considering the situation where we are willing to assume that the population distribution is a member of the family of Exponential distributions. We are interested in finding the RSD of the sample average and/or the sum.
It will turn out that sums of exponentials have a Gamma distribution. The Gamma distribution with shape parameter \(\alpha\) and rate parameter \(\beta\) has probability density function
\[ f_X(x) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\beta x} \;\;\; \alpha>0, \beta>0, x>0, \] where \(\Gamma(\cdot)\) denotes the so-called Gamma function. A random variable \(X\) that has a \(Gamma(\alpha,\beta)\) distribution has \(E[X]=\frac{\alpha}{\beta}\) and \(Var[X]=\frac{\alpha}{\beta^2}\).
The Exponential distribution is a special case of the Gamma distribution: \(\alpha=1\). As the sum of \(n\) independent \(X_i \sim Gamma(\alpha_i,\beta)\) has the \(Gamma(\sum_{i=1}^n \alpha_i, \beta)\) distribution, we have the following result:
Theorem 5 - Sums of Exponentials are Gamma:
Suppose that \(X \sim Exp(\lambda)\), and that we have a random sample \(X_1,\ldots,X_n\).
If \(X \sim Gamma(\alpha,\beta)\) then \(cX \sim Gamma(\alpha,\frac{\beta}{c})\). This results is easy to derive for Exponential distributions (\(\alpha=1\)):
\[ F_{cX}(x) = P(cX < x) = P(X < \frac{x}{c}) = 1 - e^{-\frac{\lambda}{c}x}, \] which we recognise as the cdf of an Exponential distribution with parameter \(\frac{\lambda}{c}\).
By taking \(c=2\lambda\) and \(X\sim Gamma(n,\lambda)\) we obtain the result \(2 \lambda X \sim Gamma(n, \frac{1}{2})\). This is the Chi-squared distribution with \(2n\) degrees of freedom:
Theorem 6 - The Gamma distribution can be transformed into a Chi-squared distribution:
Suppose that \(X \sim Exp(\lambda)\) so that \(Y=\sum_{i=1}^n X_i \sim Gamma(n, \lambda)\).
This result is helpful for us, because our statistical tables pdf does not include the Gamma distribution but does include the Chi-squared distribution.
The Chi-squared distribution with \(k\) degrees of freedom has mean \(k\) and variance \(2k\).
2.3.1 Aproximation using CLT
If \(X \sim Exp(\lambda)\), we know that \(E[X]=\frac{1}{\lambda}\) and \(Var[X]=\frac{1}{\lambda^2}\). The central limit theorem then states that \[\bar{X} \overset{approx}{\sim} N(\frac{1}{\lambda}, \frac{1}{n\lambda^2}).\] This implies that \[\sum_{i=1}^n X_i \overset{approx}{\sim} N(\frac{n}{\lambda}, \frac{n}{\lambda^2}).\]
For example, if \(\lambda=1\) and \(n=10\), the exact RSD of \(\sum_{i=1}^n X_i\) is \(Gamma(10,1)\), which has mean \(10\) and variance \(10\). The approximate RSD is \(N(10, 10)\).
2.4 Example 4: \(X \sim Bernoulli(p)\)
We are considering the situation where we are willing to assume that the population distribution is a member of the family of Bernoulli distributions. We are interested in finding the RSD of the sample average and/or the sum.
Suppose that we draw a random sample of size \(5\) from the Bernoulli(\(p=0.25\)) distribution:
set.seed(1234)
rbinom(5, size=1, prob=0.25)## [1] 0 0 0 0 1The probability of observing this sample is \(p^{1}(1-p)^{5-1}=0.25 \times 0.75^4\). The sum of the observations (\(Y\)) is equal to 1. This is, however, not the only way in which we can obtain a sample of 5 Bernoullis with sum equal to 1: the number of ways in which we can select 1 object from a group of 5 objects when the order is not important is:
\[ \begin{pmatrix} 5 \\ 1 \end{pmatrix} = \frac{5!}{1!4!}=5. \] The correct probability is given by the probability mass function of the so-called Binomial(\(n,p\)) distribution (where in our example \(n=5\), \(k=1\) and \(p=0.25\)):
\[ P(Y=k) = P \left( \sum_{i=1}^n X_i=k \right) = \begin{pmatrix} n \\ k \end{pmatrix} p^k(1-p)^{n-k}. \]
We have the following result:
Theorem 7 - The sum of Bernoullis is Binomial:
Suppose that \(X \sim Bernoulli(p)\), and that we have a random sample \(X_1,\ldots,X_n\).
The Binomial(\(n,p\)) distribution has mean \(np\) and variance \(np(1-p)\), n times the mean and variance of the Bernoulli distribution. It turns out that we can, in some cases, approximate the Binomial distribution by a Poisson distribution:
Theorem 8 - Approximate Binomial by Poisson:
Suppose that \(Y \sim Binomial(n,p)\), with \(n\) large and \(p\) small.
The graph below displays the pmf, the cdf and the quantile function for Binomial distributions with \(n=30\) and \(p\) ranging from \(0.1\) to \(0.9\).
Theorem 8 states that the Binomial distribution with \(n=30\) and \(p=0.1\) should be well approximated by the Poisson distribution with \(\lambda=3\):
set.seed(1234)
round( dbinom(0:10, size = 30, prob=0.1), 2)## [1] 0.04 0.14 0.23 0.24 0.18 0.10 0.05 0.02 0.01 0.00 0.00round( dpois(0:10, lambda=3), 2)## [1] 0.05 0.15 0.22 0.22 0.17 0.10 0.05 0.02 0.01 0.00 0.00The Binomial distribution with \(n=30\) and \(p=0.5\) may not be well-approximated by the Poisson distribution with \(\lambda = 15\):
set.seed(1234)
round( dbinom(10:20, size = 30, prob=0.5), 2)## [1] 0.03 0.05 0.08 0.11 0.14 0.14 0.14 0.11 0.08 0.05 0.03round( dpois(10:20, lambda=15), 2)## [1] 0.05 0.07 0.08 0.10 0.10 0.10 0.10 0.08 0.07 0.06 0.042.4.1 Approximation using CLT
If \(X \sim Bernoulli(p)\), we know that \(E[X]=p\) and \(Var[X]=p(1-p)\). The central limit theorem then states that \[\bar{X} \overset{approx}{\sim} N \left( p, \frac{p(1-p)}{n} \right).\] This implies that \[\sum_{i=1}^n X_i \overset{approx}{\sim} N(np, np(1-p)).\] The exact distribution of \(\sum_{i=1}^n X_i\) is Binomial(\(n,p\)), which also has mean \(np\) and variance \(np(1-p)\).
3 Questions About The Means (or Proportions) of Two Populations
No new RSD-results are required for questions about two means
Suppose that we have two random samples. The first random sample (\(X_{11}, \ldots X_{1 n_1}\)) is a sample of incomes from Portugal and has size \(n_1\). The second random sample ((\(X_{21}, \ldots X_{2 n_2}\))) is a sample of incomes from England and has size \(n_2\). We want to compare the mean of the income distribution in Portugal with the mean of the income distribution in England. The obvious thing to do is to compare \(\bar{X}_1\), the sample average of the Portuguese sample, with \(\bar{X}_2\), the sample average of the English sample. In particular, we would compute \(\bar{X}_1 - \bar{X}_2\). What is the repeated sampling distribution of \(\bar{X}_1 - \bar{X}_2\)? The answer will depend on what we are willing to assume about the income distributions in Portugal (\(X_1\)) and England (\(X_2\)).
3.1 Example 5: \(X_1 \sim N(\mu_1,\sigma^2_1)\) and \(X_2 \sim N(\mu_2,\sigma^2_2)\)
Suppose that we are willing to assume that both income distributions are members of the Normal family of distributions. From what we have already learned, we can state the following facts:
- As \(X_1 \sim N(\mu_1, \sigma^2_1)\), we know that \(\bar{X}_1 \sim N \left( \mu_1, \frac{\sigma^2_1}{n_1} \right)\)
- As \(X_2 \sim N(\mu_2, \sigma^2_2)\), we know that \(\bar{X}_2 \sim N \left( \mu_2, \frac{\sigma^2_2}{n_2} \right)\)
- As \(\bar{X}_1 - \bar{X}_2\) is a linear combination of Normals (with \(c_1 = 1\) and \(c_2 =-1\)), we know that \(\bar{X}_1 - \bar{X}_2\) has a Normal distribution.
- As \(E[\bar{X}_1 - \bar{X}_2]=\mu_1 - \mu_2\), we know that this Normal distribution has mean \(\mu_1 - \mu_2\).
- As \(Var[\bar{X}_1]-Var[\bar{X}_2] = \frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2} - 2 \times 0\), we know that this Normal distribution has variance \(\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}\).
Therefore, we know that
RSD of \(\bar{X}_1-\bar{X}_2\) with two Normal distributions:
if \(X_1\sim N(\mu_1,\sigma^2_1)\) and \(X_2\sim N(\mu_2,\sigma^2_2)\) then
\[\bar{X}_1 - \bar{X}_2 \sim N \left(\mu_1 - \mu_2, \frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2} \right).\]
In the special case that \(\sigma^2_1=\sigma^2_2=\sigma^2\), we have
\[\bar{X}_1 - \bar{X}_2 \sim N \left(\mu_1 - \mu_2, \sigma^2 \left\{ \frac{1}{n_1} + \frac{1}{n_2} \right\} \right).\]To calculate probabilities associated to \(RSD(\bar{X}_1-\bar{X}_2)\), we need to standardise. How we standardise will depend on whether or not \(\sigma^2_1\) and \(\sigma^2_2\) are known. If they are known, we will denote them by \(\sigma^2_{10}\) and \(\sigma^2_{20}\).
3.1.1 Variances Known: \(\sigma^2_{10}\) and \(\sigma^2_{20}\)
If the variances are known, we can standardise using the known variances and obtain a repeated sampling distribution that is standard-normal:
\[ \frac{(\bar{X}_1 - \bar{X}_2) - (\mu_1 -\mu_2)}{\sqrt{\frac{\sigma^2_{10}}{n_1} + \frac{\sigma^2_{20}}{n_2}}} \sim N(0,1). \]
3.1.2 Variances Unknown but The Same: \(\sigma^2_{1}=\sigma^2_{2}=~\sigma^2\)
If the variances \(\sigma^2_1\) and \(\sigma^2_2\) are not known, we need to estimate them. If \(\sigma^2_1\) and \(\sigma^2_2\) are unknown, but known to be equal (to the number \(\sigma^2\), say), we can estimate the single unknown variance using only the first sample or using only the second sample. It would be better, howvere, to use the information contained in both samples.
The so-called pooled adjusted sample variance (\(S^{\prime 2}_p\)) can be used to estimate \(\sigma^2\) using both samples:
\[\begin{align} S^{\prime 2}_p &=\frac{1}{n_1+n_2-2} \left\{ \sum_{i=1}^{n_1}(X_{1i}-\bar{X}_1)^2 + \sum_{j=1}^{n_2}(X_{2j}-\bar{X}_2)^2\right\} \\ &= \frac{(n_1-1)S^{\prime 2}_1 + (n_2-1)S^{\prime 2}_2}{n_1 + n_2 -2}. \end{align}\]
We already know that standardising a Normal with a single estimated variance gives a \(t\) distribution:
\[ \frac{(\bar{X}_1 - \bar{X}_2) - (\mu_1 -\mu_2)}{\sqrt{ S^{\prime 2}_p \left\{ \frac{1}{n_1} + \frac{1}{n_2}\right\} }} \sim t_{n_1 + n_2 -2}. \]
The number of degrees of freedom of the \(t\) distribution is \(n_1 + n_2 -2\) (not \(n_1 +n_2 -1\)) because \(S^{\prime 2}_p\) uses two estimates: \(\bar{X}_1\) estimates \(\mu_1\) and \(\bar{X}_2\) estimates \(\mu_2\).
3.1.3 Variances Unknown, Approximation Using CLT
If the variances \(\sigma^2_1\) and \(\sigma^2_2\) are unknown and not known to be the same, we have the estimate both of them. Standardising with two estimated variances does not lead to a \(t\) distribution, so we have no exact RSD. We can approximate the RSD using the Central Limit Theorem:
- \[\bar{X}_1 - \bar{X}_2 \overset{approx}{\sim} N \left(\mu_1 - \mu_2, \frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2} \right).\]
Standardising with two estimated variances gives:
\[ \frac{(\bar{X}_1 - \bar{X}_2) - (\mu_1 -\mu_2)}{\sqrt{\frac{S^{\prime 2}_1}{n_1} + \frac{S^{\prime 2}_2}{n_2}}} \overset{approx}{\sim} N(0,1). \]
- Note that this approximate result is correct for any population distribution \(X_1\) and \(X_2\). They do not need to be Normal distributions. In Example 6 we will use this result using Bernoulli population distributions.
- Note also that, apparently, for the large sample approximation it does not matter if \(\sigma^2_1\) and \(\sigma^2_2\) are known or estimated.
- If the sample is rather small, the approximation obtained using the CLT can be slightly improved by using the so-called Welch Approximation. We will not go into this.
3.2 Example 6: \(X_1 \sim Bernoulli(p_1)\) and \(X_2 \sim Bernoulli(p_2)\)
We are now assuming that \(X_1\) and \(X_2\) both have Bernoulli distributions. For example, \(p_1\) could represent the unemployment rate in Portugal and \(p_2\) the unemployment rate in England. In that case we would base our analysis of \(p_1-p_2\) on \(\bar{X}_1 - \bar{X}_2\), the difference of the fraction of unemployed in sample 1 with the fraction of unemployed in sample 2. The central limit theorem states that both sample averages have an RSD that is approximately Normal. As \(\bar{X}_1 - \bar{X}_2\) is a linear combination of (approximately) Normal, its RSD is (approximately) Normal.
Section 3.1.1 tells us how to standardise with known variances:
\[ \frac{(\bar{X}_1 - \bar{X}_2) - (p_1 - p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}} \overset{approx}{\sim} N(0,1), \] where we have used that, for Bernoulli distributions, \(\mu=p\) and \(\sigma^2=p(1-p)\). Moreover, we can estimate \(p\) by \(\bar{X}\). Using section 3.1.3, standardising with the estimated variances gives:
\[ \frac{(\bar{X}_1 - \bar{X}_2) - (p_1 - p_2)}{\sqrt{\frac{\bar{X}_1(1-\bar{X}_1)}{n_1} + \frac{\bar{X}_2(1-\bar{X}_2)}{n_2}}} \overset{approx}{\sim} N(0,1). \]
4 Questions About The Variance of A Single Population
The 3 most important RSD-results for questions about the variance will turn out to be:
- sum of standard-normal-squared is Chi-squared(\(n\))
- Estimate \(r\) parameters: substract \(r\) from the number of degrees of freedom
- This implies: \(\frac{(n-1)S^{\prime 2}}{\sigma^2}\) is Chi-squared(\(n-1\))
4.1 Example 7: \(X \sim N(\mu,\sigma^2)\):
We are considering the situation where we are willing to assume that the population distribution is a member of the family of Normal distributions. Instead of the mean, we are now interested in the variance of the population distribution. The obvious estimator of the unknown population variance is the adjusted sample variance \(S^{\prime 2}=\frac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2\). We are interested in finding the RSD of the sample variance.
Theorem 9 - The sum of squares of standard-normals is Chi-squared:
Suppose that \(X \sim N(0,1)\), and that we have a random sample \(X_1,\ldots,X_n\).
Note: if we have a random sample from \(N(\mu,\sigma^2)\), we can standardise:
\[\begin{align} Y &= \sum_{i=1}^n \left( \frac{X_i-\mu}{\sigma} \right)^2 \\ &= \frac{\sum_{i=1}^n (X_i-\mu)^2}{\sigma^2} \\ &= \frac{(n-1) S^{\prime 2}_{\mu}}{\sigma^2} \sim \chi^2_{n}. \end{align}\] where \(S^{\prime 2}_{\mu}=\frac{1}{n-1}\sum_{i=1}^n (X_i - \mu)^2\) denotes the adjusted sample variance using a \(\mu\) that has to be known.The adjusted sample variance using \(\mu\) (\(S^{\prime 2}_{\mu}\)) cannot be used in practice to estimate \(\sigma^2\) because the value of \(\mu\) is typically unknown. The adjusted sample variance \(S^{\prime 2}\) uses \(\bar{X}\) to estimate this unknown \(\mu\). A Chi-squared random variable loses one degree of freedom as a result of estimating one unknown parameter (it would lose \(r\) degrees of freedom as a result of estimating \(r\) unknown parameters):
Theorem 10 - Estimate r parameters: lose r degrees of freedom:
Suppose that \(X \sim N(\mu,\sigma^2)\), and that we have a random sample \(X_1,\ldots,X_n\).
To summarise this section: although we did not find the repeated sampling distribution of the adjusted sample variance \(S^{\prime 2}\), we were able to derive the repeated sampling distribution of \(\frac{(n-1)S^{\prime 2}}{\sigma^2}\). This result will turn out to be sufficient.
4.2 Aproximation using CLT
We will only consider the Normal population distribution for questions about the population variance.
5 Questions About The Variances of Two Populations
The 2 most important RSD-results for questions about two variances will turn out to be:
- \(\frac{Chi-squared(a)/a}{Chi-squared(b)/b}\) is \(F_{a,b}\)
- This implies: \(\frac{S_1^{\prime 2} / \sigma^2_1 }{ S_2^{\prime 2} / \sigma^2_2} \sim F_{n_1-1, n_2-1}\)
Suppose that we have two random samples. The first random sample (\(X_{11}, \ldots X_{1 n_1}\)) is a sample of incomes from Portugal and has size \(n_1\). The second random sample (\(X_{21}, \ldots X_{2 n_2}\)) is a sample of incomes from England and has size \(n_2\). We want to compare the variance of the income distribution in Portugal with the variance of the income distribution in England. The obvious thing to do is to compare \(S^{\prime 2}_1\), the adjusted sample variance of the Portuguese sample, with \(S^{\prime 2}_2\), the adjusted sample variance of the English sample. In particular, we would compute \(S^{\prime 2}_1 -S^{\prime 2}_2\). Unfortunately, there is no easy way to obtain the repeated sampling distribution of \(S^{\prime 2}_1 -S^{\prime 2}_2\).
If we assume that both population distributions are Normal, we can derive a result that comes close enough.
5.1 Example 8: \(X_1 \sim N(\mu_1,\sigma^2_1)\) and \(X_2 \sim N(\mu_2,\sigma^2_2)\)
Instead of investigating whether or not \(S^{\prime 2}_1 -S^{\prime 2}_2\) is close to zero, we can also investigate whether or not \(S^{\prime 2}_1 / S^{\prime 2}_2\) is close to \(1\). What can be proved is the following:
Theorem 11 - F-distribution:
Suppose that \(X_1 \sim N(\mu_1,\sigma^2_1)\) and \(X_2 \sim N(\mu_2,\sigma^2_2)\) and that
we have a random sample of size \(n_1\) from the first population distribution and a random sample of size \(n_2\) from the second population distribution.
Clearly, \(\frac{S^{\prime 2}_2 / \sigma^2_2}{S^{\prime 2}_1 / \sigma^2_1} \sim F_{n_2-1,n_1-1}\). The F distribution has another property that is related to quantiles: let \(q_p^{F_{n_1,n_2}}\) denote the \(p\) quantile of the \(F\) distribution with degrees of freedom \(n_1\) and \(n_2\). Then, \[ q_p^{F_{n_1,n_2}} = \frac{1}{q_{1-p}^{F_{n_2,n_1}}}. \] For example, let’s calculate the \(0.05\) quantile (or: \(5\%\) quantile) of the \(F_{10,20}\) distribution:
qf(0.05, df1=10, df2=20)## [1] 0.3604881Now, we calculate 1 over the \(95\%\) quantile of the \(F_{20,10}\) distribution:
1 / qf(0.95, df1=20, df2=10)## [1] 0.36048815.2 Aproximation using CLT
We will only consider the Normal population distributions for questions about the ratio of population variances.
6 Questions about the Maximum or Minimum (Order Statistics)
Consider a random sample of size \(n\): \(X_1,X_2, \ldots ,X_n\). If we were to sort the sample in ascending order, we obtain the so-called order statistics \(X_{(1)}, X_{(2)}, \ldots , X_{(n)}\). Hence, the minimum value that will be obtained in the sample is denoted by \(X_{(1)}\) and the maximum value that will be obtained in the sample is denoted by \(X_{(n)}\).
Sometimes we are more interested in the repeated sampling distribution of the maximum value that occurs in a sample than in the population mean or the population variance. For instance, if we build a dike to protect us from possibly rising sea-levels due to global warming, we are interested in the probability that the maximum sea-level in a sample of \(n\) months is larger than the heigth of the dike. This is an interesting question because, if this probability is high, we are likely to all drown.
We can link the cumulative distribution function of the RSD of the maximum value in the sample (\(F_{X_{(n)}}(x)\)) with the cumulative distribution of the population distribution (\(F_X(x)\)) by noting the following: the maximum value obtained in the sample is smaller than \(x\) if all values in the sample are smaller than \(x\):
\[\begin{align} F_{X_{(n)}}(x) &= P(X_{(n)} < x) \\ &= P(X_1<x, \ldots, X_n < x) \\ &\overset{ind.}{=} P(X_1<x)P(X_2<x) \cdots P(X_n<x) \\ &\overset{id.}{=} \{P(X<x)\}^n \\ &= \{F_X(x)\}^n. \end{align}\]
Suppose that the dikes are 15 meters high and we measure the sea level monthly for a year. If sea-levels follow an Exponential distribution with \(\lambda=0.1\), then \(P(X_{(12)} < 15) = \{ 1 - e^{-0.1*15}\}^{12}=0.048\), about \(5\%\). The dikes are (almost certainly) too low.
In other cases, we are more interested in the repeated sampling distribution of the minimum value obtained in a sample of size \(n\) (for instance, if you sell oxygen bottles to a group of \(n\) rather agressive looking divers that ask you how long the oxygen will last “for sure”).
We can link the cumulative distribution function of the RSD of the minimum value in the sample (\(F_{X_{(1)}}(x)\)) with the cumulative distribution of the population distribution (\(F_X(x)\)) by noting the following: the minimum value obtained in the sample is larger than \(x\) if all values in the sample are larger than \(x\):
\[\begin{align} F_{X_{(1)}}(x) &= P(X_{(1)}<x) \\ &= 1 - P(X_{(1)}>x) \\ &= 1- P(X_1>x, \ldots ,X_n>x) \\ &\overset{ind.}{=} 1-P(X_1>x) P(X_2>x) \cdots P(X_n>x) \\ &\overset{id.}{=} 1-\{P(X>x)\}^n \\ &= 1 - \{1- F_X(x)\}^n. \end{align}\]
Suppose that there are 20 divers that end up diving for 2 hours and 20 minutes (140 minutes), following your suggestion. If the number of minutes that a bottle provides oxygen follows a Normal distribution with mean 155 minutes and variance of 100, then
\[\begin{align} P(X_{(1)} > 140) &= 1 - P(X_{(1)} < 140) \\ &= 1 - ( 1 - \{1- F_X(140)\}^{20}) \\ &= \left\{ 1- F_X(140) \right\}^{20} \\ &= \left\{ 1 - P \left( \frac{X - 155}{\sqrt{100}} < \frac{140 - 155}{\sqrt{100}} \right) \right\}^{20} \\ &= \{1 - \Phi(-1.5) \}^{20} \\ &= 0.25. \end{align}\]
The probability that all divers have enough oxygen is only about \(25\%\). You better run…
Note that \(P(X>140)=1-F_X(140)=1-\Phi(\frac{140-155}{10})=1-\Phi(-1.5)=0.93\). Each bottle in itself was very likely to give enough oxygen.